Numerical range
In the mathematical field of linear algebra and convex analysis, the numerical range of a square matrix with complex entries is a subset of the complex plane associated to the matrix. If A is an n × n matrix with complex entries, then the numerical range of A is the set
where x* denotes the Hermitian adjoint of the vector x. In other words, it is the range of the Rayleigh quotient. The numerical range is also called the field of values.[1]
Contents |
Numerical radius
In a way analogous to spectral radius, the numerical radius of an operator T on a complex Hilbert space, denoted by 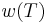 , is defined by
, is defined by
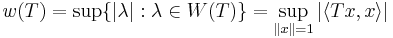 .
.
w is then a norm. It is equivalent to the operator norm by the inequality:
Paul Halmos conjectured:
for every integer 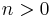 . It was later confirmed by Charles Berger and Carl Pearcy.[2]
. It was later confirmed by Charles Berger and Carl Pearcy.[2]
Some theorems
The Hausdorff–Toeplitz theorem states that the numerical range of any matrix is a convex set.[3] Furthermore, the spectrum of A is contained within the closure of W(A).[4] If A is a normal matrix, then the numerical range is the polygon in the complex plane whose vertices are eigenvalues of A.[5] In particular, if A is Hermitian then the polygon reduces to the segment of the real axis bounded by the smallest and the largest eigenvalue,
which explains the name numerical range. If A is not normal, then a weaker property holds: any "corner" of the numerical range is an eigenvalue of A. Here, the precise definition of a "corner" is that of a sharp point: a point w on the boundary of a set S ⊂ C is called a sharp point of S if there exist two angles θ1 and θ2 with 0 ≤ θ1 < θ2 < 2π such that for all z ∈ S and for all θ ∈ (θ1, θ2) the inequality Re eiθw ≥ Re eiθz holds.[6]
Bounded operators on a Hilbert space
If the closure of the numerical range of a bounded operator coincides with the convex hull of its spectrum, then it is called a convexoid operator. An example of such an operator is a normal operator.
Special cases
- matrices of order N=2. Numerical range of any operator A of order two forms an elliptical disk in the complex plane with both eigenvalues
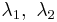 as foci and minor axis equal to
as foci and minor axis equal to 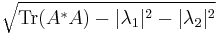 . In the special case of a normal A the disk reduces to an interval,
. In the special case of a normal A the disk reduces to an interval, ![[\lambda_{1}, \ \lambda_{2} ]](/2012-wikipedia_en_all_nopic_01_2012/I/2d8527c79a72a95bbce3ba5aa6b82514.png) - see Li 1996.
- see Li 1996.
- matrices of order N=3. Numerical range forms a) an ellipse; b) has an ovular shape; c) has a flat portion of its boundary; d) is a convex hull of a point and an ellipse e) is a triangle (for normal operators only) - see Keeler, Rodman and Spitkovsky 1997.
Generalisations
- C - numerical range
- Higher rank numerical range
- Joint numerical range
- Product numerical range
See also
Notes
- ^ Horn & Johnson (1991, Definition 1.1.1)
- ^ Lax, Linear algebra and its applications, 2nd ed.
- ^ Horn & Johnson (1991, Property 1.2.2)
- ^ Horn & Johnson (1991, Property 1.2.6)
- ^ Horn & Johnson (1991, Property 1.2.9)
- ^ Horn & Johnson (1991, Theorem 1.6.3)
References
- Horn, Roger A.; Johnson, Charles R. (1991), Topics in Matrix Analysis, Cambridge University Press, ISBN 978-0-521-46713-1.
- Li, C.K. (1996), "A simple proof of the elliptical range theorem", Proc. Am. Math. Soc. 124, 1985.
- Keeler, Dennis S.; Rodman, Leiba; Spitkovsky, Ilya M. (1997), "The numerical range of
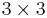 matrices", Linear Algebra Applications 252, 115.
matrices", Linear Algebra Applications 252, 115.
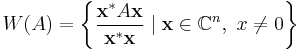
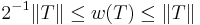
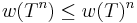
![W(A) \ = \ [\lambda_{\rm min}, \ \lambda_{\rm max} ]](/2012-wikipedia_en_all_nopic_01_2012/I/50f852f1fbd294df2dd9fd832428b713.png)